作者:郭鑫(上海复旦规划建筑设计研究院有限公司主任工程师,本中心特聘研究员)
多维时间序列数据是随着时间的前进、事物无时无刻的变化而产生的。从一个人的手指在空间中xyz三轴的坐标变化,到某城市历年来三次产业增加值的变迁,再到气象站各种气象数据的多年积累——这种具有多个含义属性且具有时间长度的数据就是多维时间序列数据。

然而,职能手环如何判断你以开始某种健身?多个城市间的产业构成是否重复?以及如何划分近年全球的大气成分相似区?这便需要将多个多维时间序列进行聚类计算以求其相似性。它可以用来帮助分析判断多个被研究单位之间是否存在共同的趋势,对数据所揭示的潜在规律提供有力的支撑和可信的证据。
目前,对于一维时间序列相似度的计算,通常认为对于真实数据,DTW(Dynamic Time Warping,动态时间规整)效果较优:Shen等(2021)认为DTW通过非线性翘曲能够找到两条时间序列间的最佳对齐方式,实现两序列对齐点的累差(accumulated differences)最小化[[i]];Lampert等(2018)认为正因这一特征,DTW胜过其他计算最优中心点的聚类算法,例如k-Means等[[ii]]。
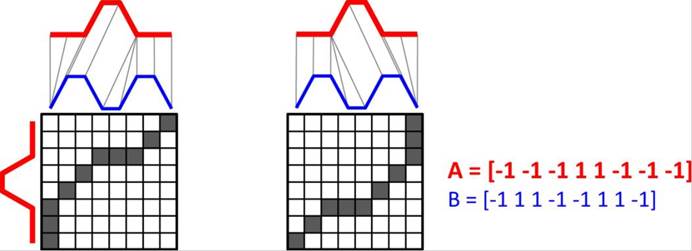
近年来,为提高聚类的准确性,解决“两序列形状相似但所处位置不同会被认为有较大差异”这一问题[[iii]],经宇毅(2019)提出了有效的改进算法,即通过计算两序列的最长公共子串引入了衰减系数。
然而,只能计算一维的时间序列数据的相似性,这在城市研究中也是远远不够的。眼下常见的做法是通过PCA(主成分分析)等算法将数据降至1维。但是在降维后,会无法避免的丢失一部分信息。虽然对于多维时间序列,DTW可以使用两种不同方式进行处理:独立与非独立翘曲(dependent or independent warping)。但“两序列形状相似但所处位置不同会被认为有较大差异”这一问题却又变得无法解决。尤其是在城市研究中,这一缺陷意味着将发展模式相似、但所处发展阶段不同的城市识别为完全不同的类型——这是完全不能接受的。
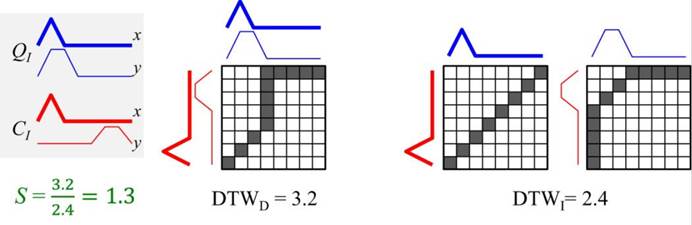
因此,笔者提出了一种融合了多维时间序列公共子串识别的DTWD方法,并结合机器学习算法组合成一套适用于城市研究的多维时间序列相似性计算工作流,暂且命名为A-DTWD(Attenuating Dynamic Time Warping with Dependent Warping)。接下来,用河南省37个城市[1]的建设用地面积数据[2]来做尝试,数据的形状为“18个年份×37个城市×8种用地面积”。
在经过计算后,可以发现通过本方法计算而聚类出的结果,具有比传统方法更高的轮廓系数(Silhouette score),并且在控制分类结果类别数量时发现了有趣结果。
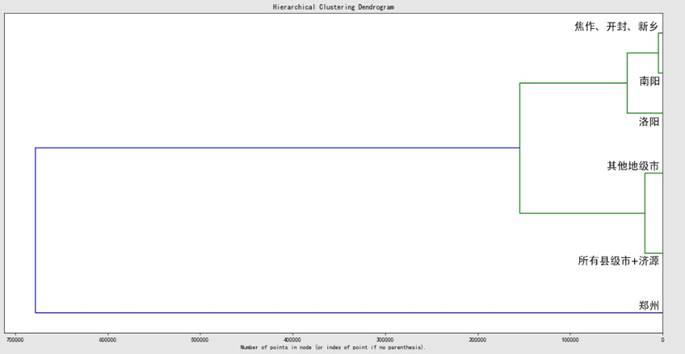
将分类结果控制为2类时,省会郑州被单独识别出来,意即河南各城市中建设用地组成及变化最为独特的城市。作为1954年设立的省会城市,并且也是中原城市群和郑州大都市区的核心城市,其对河南及周边地区有着强大的极化效应,其常住人口增速以及经济发展在省内独树一帜,因此推断其建设用地的使用方式最为独特。
在将分类结果控制为3类时,焦作、开封、南阳、新乡、洛阳5个地级市作为一个相对独特的整体被识别出来。除南阳外(稍后单独阐述),其他4个城市都紧邻省会郑州,位于中原城市群的核心部位,其与省会郑州的经济与社会联系紧密,是河南省的发展中心。同时这些城市皆位于京广线、陇海线及焦柳线等国家Ⅰ级客货共线铁路上,也是整个国家东与西、南与北交流的重要核心。
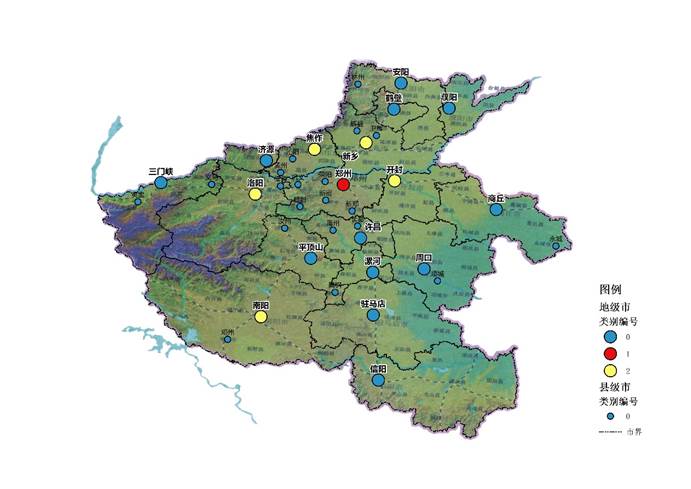
将分类结果控制为4类时,洛阳被从这5个城市中独立出来。洛阳为十三朝古都,加上建国初期国家将156个重点建设项目中的7项放在洛阳,将洛阳定位于新兴工业城市,从而奠定了现代洛阳城市的发展路径。此外,在其第三期总体规划中,城市总体布局有20世纪80年代单一带状城市改变为与自然环境有机融合的组团式带状城市结构。2006年规划则确定了远期跨河、开拓新的城市发展方向,形成“五区一团”分片组团式的用地布局,“一主两副”的城市中心——这些发展特征在河南城市中是绝无仅有的[[iv]]。
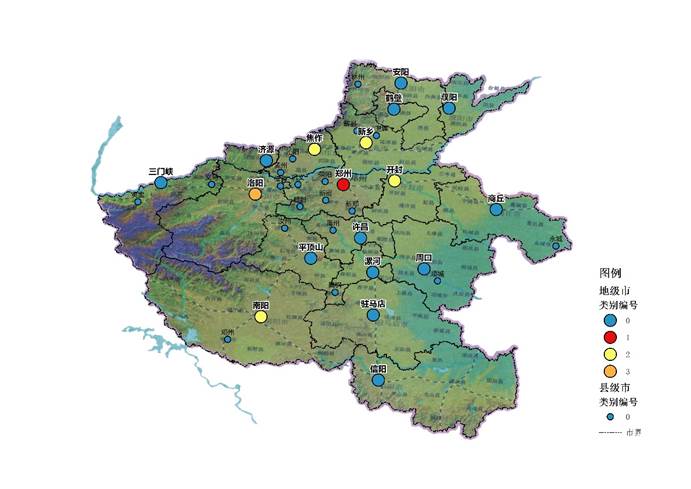
在将分类结果控制为5类时,其余11个地级市被识别成新的一类,剩下的为所有县级市和济源市。其中济源市2005年升格为省辖市,虽按正地级市所有行政管理机构配置,但其各方面体量仍和其他传统地级市有所差距。所以,此处再次体现了行政等级差异在用建设用地使用上的影响力,并且这一影响力会持续较长时间。
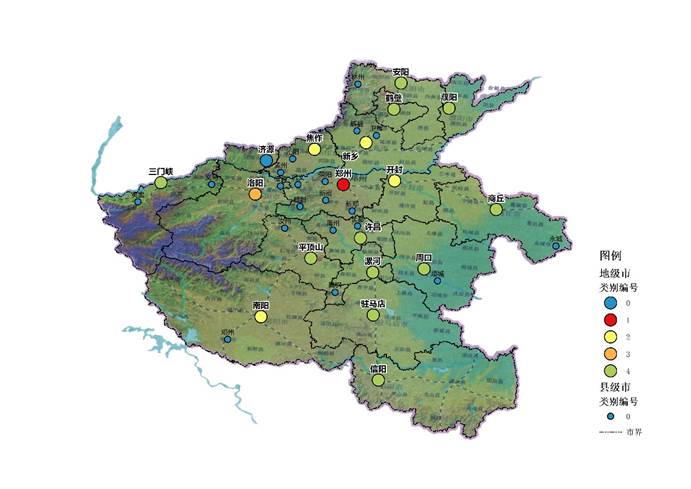
在将分类结果控制为6类时,南阳从3类时识别出的5个城市中独立出来。因地处河南西南部南阳盆地,南阳市区位在省内自成一隅,其大部地区属长江、淮河流域,自古人口众多,其与湖北省尤其襄阳地区无论在文化还是经济上的联系也十分紧密。
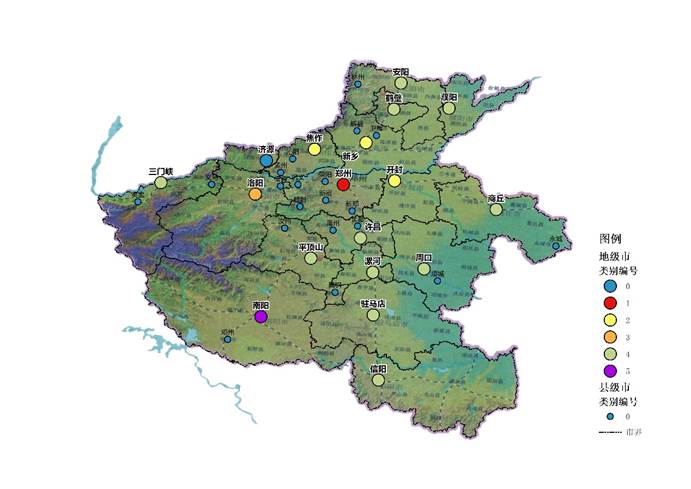
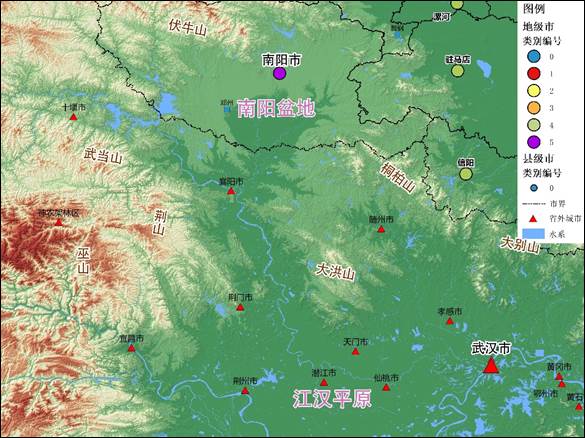
看到这里的大家请注意,计算所使用的数据是不含任何地理位置信息的仅有每个城市每类建设用地的历年绝对数值。然而,计算结果不仅体现出了与地理空间位置、地貌、地缘紧密相关的空间分布特征,也体现出了行政等级、历史积淀及现代重大政策给城市建设所带来的影响。由此可以印证,本多维时间序列聚类方法可以帮助我们更好地发现比较多个事物之间的距离与相似,识别共同趋势与潜在关系。而针对城市研究的多维时间序列聚类计算,也可进一步应用到用地绩效评价、城市群内部类型结构划分、试点城市批次选择、产业相似度计算、同类型城市发展经验借鉴,以及基于有监督学习的用地变化轨迹(land use change trajectories)模拟及预测等一系列研究中。
[1]原表中包含省会城市、地级市和县级市共39个。由于长垣市仅有2019年的数据,而登封市数据异常过多无法修复,因此将其剔除。参加计算的城市共计37个。
[2]《年鉴》中指城市用地中除水域与其他用地之外的各项用地面积,统计范围为设市的城市的城区:a.街道办事处所辖地域;b.城市公共设施、居住设施和市政公用设施等连接到的其他镇(乡)地域;c.常住人口在3000人以上独立的工矿区、开发区、科研单位、大专院校等特殊区域。
[[i]]Shen D,Chi M. TC-DTW: Accelerating Multivariate Dynamic Time Warping Through Triangle Inequality and Point Clustering[J]. 2021. http://arxiv.org/abs/2101.07731

